阅读与思考
矩形、菱形、正方形都是平行四边形,但它们都是有特殊条件的平行四边形,正方形不仅是特殊的平行四边形,而且是邻边相等的特殊矩形,也是有一个角是直角的菱形,因此,我们可以利用矩形、菱形的性质来研究正方形的有关问题.
正方形问题常常转化为三角形问题解决,在正方形中,我们最容易得到特殊三角形、全等三角形,熟悉以下基本图形.
例题与求解
【例l】 如图,在正方形纸片ABCD中,对角线AC,BD 交于点O ,折叠正方形纸片ABCD ,使 AD落在 BD上,点 A恰好与BD 上的点F 重合,展开后,折痕DE 分别交AB , AC于点E ,G .下列结论:①∠AGD=112.5° ;②AD/AE=2 ;③S△AGD=S△OGD ;④四边形AEFG 是菱形;⑤ BE=2OG.
其中,正确结论的序号是______________.
【例2】如图1,操作:把正方形CGEF 的对角线 CE放在正方形 ABCD的边BC 的延长线上(CG>BC)
,取线段AE 的中点M .连MD ,MF .
(1)探究线段MD ,MF 的关系,并加以证明.
(2)将正方形CGEF 绕点C 旋转任意角后(如图2),其他条件不变.探究线段 MD,MF 的关系,并加以证明.
【例3】如图,正方形ABCD 中,E , F是 AB,BC 边上两点,且 EF=AE+FC,DG⊥EF 于G ,求证:DG=DA .
【例4】 如图,正方形 ABCD被两条与边平行的线段EF 、GH 分割成四个小矩形, P是EF 与GH 的交点,若矩形PFCH 的面积恰是矩形AGPE 面积的2倍,试确定∠HAF的大小,并证明你的结论
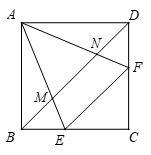
【例5】 如图,在正方形 ABCD中,E ,F 分别是边BC ,CD 上的点,满足EF=BE+DF ,AE,AF
分别与对角线BD 交于点M,N .
求证:(1)∠EAF=45 °;
(2) MN²=BM²+DN².
【例6】已知 :正方形ABCD 中,∠MAN=45° ,∠MAN 绕点 A顺时针旋转,它的两边分别交 CB,DC (或它们的延长线)于点 M,N.
当∠MAN 绕点 A旋转到BM=DN 时(如图1),易证 BM+DN=MN.
(1)当 ∠MAN绕点 A旋转到 BM≠DN时(如图2),线段 BM和DN 之间有怎样的数量关系?写出猜想,并加以证明;
(2)当∠MAN 绕点A 旋转到如图3的位置时,线段BM,DN 和 MN之间又有怎样的数量关系?请直接写出你的猜想.
更多例题与解析,请免费下载: