转着按：真正的教育，当然不止发生在大学，也不止发生在学校。作者建议人的健康、人与人亲近，都是非常好的建议。但是奈何上位管理者，希望每个学生都是独立的，互相竞争的，并不鼓励学生之间的合作。所以真正的…
年度归档： 2023 年
【提招专题】全等三角形 模型4——平行线中点模型
全等三角形模型繁杂，本次的内容是全等三角形的第四个模型——平行线中点模型，即在一组平行线中找出两个全等三角形，并证明和解决各种问题。 平行线中找到全等三角形不难，如何运用并解决实际问题才是关键： …
【提招专题】全等三角形 模型3—— 倍长中线模型
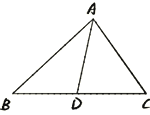
全等三角形模型繁杂，本次的内容是全等三角形的第三个模型——倍长中线模型，即三角形的某个顶点的中线，要小于与这个顶点有关的两边长之和的二分之一。 那么，这一结论与全等三角形有何关系？又如何运用呢？ …
【提招专题】全等三角形 模型2—— 手拉手模型
全等三角形模型繁杂，本次的内容是全等三角形的第二个模型——手拉手模型，即两个全等三角形有顶点重合。 那么，如何快速找出有顶点重合的两个三角形并证明它们全等呢？ 模型讲解 …
【提招专题】全等三角形 模型1—— K型模型
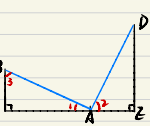
全等三角形是初中几何的基础内容。虽然基本证明公理计较简单，但是在较复杂模型中，要能快速和准备应用全等三角形模型，仍然是一件不容易的事情。 全等三角形的好处是，通过三角形全等，可以实现由边相等证明角…
昆山友果暑假班教学计划 — 六年级数学
友果暑假班教学计划 六年级数学 课次 内容 1 长方体和正方体的认识 2 长方体和正方体的表面积和体积 3 面积和单位的换算 4 长方体和正方体复习 5 分数乘法1 6 分数乘法2 7 分数除法1…
昆山市新初一 分班考试 入校测试 模拟试题（语文+数学+英语, pdf）
现在初一的新生，都面临分班的问题。分班之前，都会对学生做一个初步的测试，以此作为分班的依据。 分班考试一般在8月份举行。 分班考试的科目是：语文 + 数学 + 英语 分班考试的内容，…
【提招专题】最值问题——将军饮马
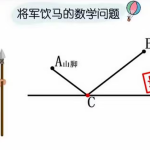
暑假期间，很多同学自学了《轴对称图形》这一章节。轴对称图形虽然看起来简单，但其实对解决问题帮助很大。 今天给大家介绍利用轴对称思想解决最值问题的经典方法——将军饮马。 …
昆山友果2023年秋季周末小班课程表——初一语文培训 | 初一数学培训 | 初一英语培训
友 果 小 班 2023年秋季小班课程表 （小班3—6人） 初一 科目 时间 初一数学 周六上午 8:30-10:00 初一英语 周六上午10:05-11:35 初一语文 周六下午 1:00 …