阅读与思考
平行四边形、矩形、菱形的性质定理与判定定理是从对边、对角、对角线三个方面探讨的,矩形、菱形都是特殊的平行四边形,矩形的特殊性由一个直角所体现,菱形的特殊性是由邻边相等来体现,因此它们除兼有平行四边形的一般性质外,还有特有的性质;反过来,判定一个四边形为矩形或菱形,也就需要更多的条件.
连对角线后平行四边形、矩形、菱形就与特殊三角形联系在一起,所以讨论平行四边形、矩形、菱形相关问题时,常用到特殊三角形性质、全等三角形法;另一方面,又要善于在四边形的背景下思考问题,运用平行四边形、矩形、菱形的丰富性质为解题服务,常常是判定定理与性质定理的综合运用.
熟悉以下基本图形:
例题与求解
【例l】如图,矩形ABCD的对角线相交于O,AE平分∠BAD,交BC于E,∠CAE=15°,那么∠BOE=________.
【例2】下面有四个命题:
①一组对边相等且一组对角相等的四边形是平行四边形;
②一组对边相等且一条对角线平分另一条对角线的四边形是平行四边形;
③一组对角相等且这一组对角的顶点所连结的对角线平分另一条对角线的四边形是平行四边形;
④一组对角相等且这一组对角的顶点所连结的对角线被另一条对角线平分的四边形是平行四边形;
其中,正确的命题的个数是( )
A.1 B. 2 C. 3 D.4
【例3】如图,菱形ABCD的边长为2,BD=2,E,F分别是边AD,CD上的两个动点且满足AE+CF=2.
(1)判断△BEF的形状,并说明理由;
(2)设△BEF的面积为S,求S的取值范围.
【例4】如图,设P为等腰直角三角形ACB斜边AB上任意一点,PE⊥AC于点E,PF⊥BC于点F,PG⊥EF于点G,延长GP并在春延长线上取一点D,使得PD=PC.
求证:BC⊥BD,BC=BD.
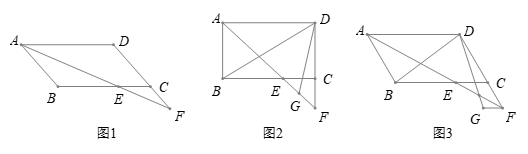
【例5】在□ABCD中,∠BAD的平分线交直线BC于点E,交直线DC的延长线于点F.
(1)在图1中证明CE=CF;
(2)若∠ABC=90°,G是EF的中点(如图2),直接写出∠BDG的度数;
(3)若∠ABC=120°,FG∥CE,FG=CE,分别连结DB,DG(如图3),求∠BDG的度数.
【例6】如图,△ABC中,∠C=90°,点M在BC上,且BM=AC,点N在AC上,且AN=MC,AM与BN相交于点P.
求证:∠BPM=45°.
更多例题及解析请免费点击下载: