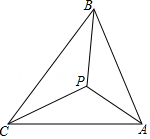
1．法国数学家费马提出：在
内存在一点P，使它到三角形顶点的距离之和最小。人们称这个点为费马点，此时PA+PB+PC的值为费马距离。经研究发现：在锐角
中，费马点P满足
，如图，点P为锐角
的费马点，且PA=3，PC=4，
，则费马距离为 。
2．在
中，
，点P为
内一点。
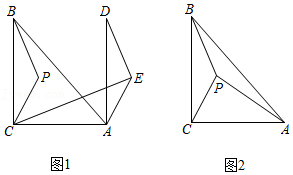
（1）如图1，连接PB，PC，将
沿射线CA方向平移，得到
，点B，C，P的对应点分别为点D，A，E，连接CE。如果
，BP=3，AB=6，则CE= 。
（2）如图2，连接PA，PB，PC，当AC=BC=8时，求PA+PB+PC的最小值。
3．如图，在
中，AB=3，AC=2，
，P 为
内一点，则PA+PB+PC的最小值为 。
点击以下链接，可以直接下载pdf文档
