阅读与思考
直角三角形是一类特殊三角形,有以下丰富的性质:
角的关系:两锐角互余;
边的关系:斜边的平方等于两直角边的平方和;
边角关系: 所对的直角边等于斜边的一半.
这些性质广泛应用于线段计算、证明线段倍分关系、证明线段平方关系等方面.
在现阶段,勾股定理是求线段的长度的主要方法,若图形缺少条件直角条件,则可通过作辅助垂线的方法,构造直角三角形为勾股定理的应用创造必要条件;运用勾股定理的逆定理,通过代数方法计算,也是证明两直线垂直的一种方法.
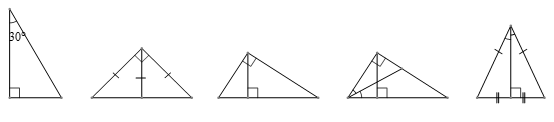
熟悉以下基本图形基本结论:
例题与求解
【例l】(1)直角△ABC三边的长分别是x, x+1 和5,则△ABC的周长=_____________.△ABC的面积=_____________.
(2)如图,已知Rt△ABC的两直角边AC=5,BC=12,D是BC上一点,当AD是∠A的平分线时,则CD=_____________.
【例2】如图所示的方格纸中,点A,B,C,都在方格线的交点,则∠ACB=( )
A.120° B.135° C.150° D.165°
【例3】如图,P为△ABC边BC上的一点,且PC=2PB,已知∠ABC=45°,∠APC=60°,求∠ACB的度数.
【例4】如图,在△ABC中,∠C=90°,∠A=30°,分别以AB,AC为边在△ABC的外侧作等边△ABE和等边△ACD,DE与AB交于F,求证:EF=FD.
【例5】如图,在四边形ABCD中,∠ABC=30°,∠ADC=60°,AD=CD,求证: BD2+AB2=BC2
【例6】斯特瓦尔特定理:如图,设D为△ABC的边BC上任意一点,a,b,c为△ABC三边长,则AD2=1\a(b2BD+c2DC) -BD.DC 请证明结论成立.
详细答案与更多习题请免费下载: