阅读与思考
等腰三角形是一类特殊三角形,具有特殊的性质,这些性质为角度的计算、线段相等、直线位置关系的证明等问题提供了新的理论依据.因此,在解与等腰三角形相关的问题时,除了要运用全等三角形知识方法外,又不能囿于全等三角形,应善于利用等腰三角形的性质探求新的解题途径,应熟悉以下基本图形、基本结论.
⑴ 图1中,∠A=180°-2∠B ,∠B=∠C=(180°-∠A)/2,∠DAC=2∠B=2∠C .
⑵ 图2中,只要下述四个条件:
①AB=AC ;②∠1=∠2 ;③CD=DB ;④AD⊥BC 中任意两个成立,就可以推出其余两个成立.
例题与求解
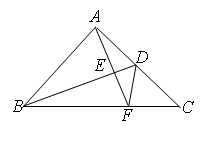
【例1】如图,在△ABC中,D在AC上,E在AB上,且AB=AC,BC=BD,AD=DE=BE,则∠A=___________.
【例2】如图,在△ABC中,已知∠BAC=900,AB=AC,D为AC中点,AE⊥BD于E,延长AE交BC于F,求证:∠ADB=∠CDF.
【例3】如图,在△ABC中,AC=BC,∠ACB=900,D是AC上一点,且AE垂直BD的延长线于E,又AE= BD,求证:BD是∠ABC的角平分线.
【例4】如图,在△ABC中,∠BAC=∠BCA=440,M为△ABC内一点,使∠MCA=300,∠MAC=160,求∠BMC度数.
【例5】如图,△ABC是边长为1的等边三角形,△BDC是顶角∠BDC=1200的等腰三角形,以D为顶点作一个600角,角的两边分别交AB于M,交AC于N,连结MN,形成一个三角形.求证:△AMN的周长等于2.
【例6】如图,△ABC中,∠ABC=460,D是BC边上一点,DC=AB,∠DAB=210,试确定∠CAD的度数.
能力训练
A级
1.如果等腰三角形一腰上的高另一腰的夹角为450,那么这个等腰三角形的底角为_____________.
2.如图,已知∠A=150,AB=BC=CD=DE=EF,则∠FEM=_____________.
3.如图,在等边△ABC的AC,BC边上各取一点P、Q,使AP=CQ,AQ,BP相交于点O,则
∠BOQ=____________.
4.如图,在△ABC中,∠BCA=900,∠BAC=600,BC=4,在CA的延长线取点D,使AD=AB,则D,B两点之间的距离是____________.
5.如图,在△ABC中,AB=AC,D为BC上一点,BF=CD,CE=BD,那么∠EDF等于( )
A.900– ∠A B.900-∠A C.1800-∠A D.450– ∠A
6.如图,在△ABC中,∠ACB=900,AC=AE,BC=BF,则∠ECF=( )
A.600 B.450 C.300 D.不确定
7.△ABC的一个内角的大小是400,且∠A=∠B,那么∠C的外角的大小是( )
A.1400 B.800或1000 C.1000或1400 D.800或1400
8.三角形三边长 , , 满足 ,则三角形一定是( )
A.等边三角形 B.以 为底边的等腰三角形
C.以 为底边的等腰三角形 D.等腰三角形
更多习题及答案解析请免费下载: