1、我们知道,任意一个一次函数的图象都是平面上的一条直线,那么,是不是平面上的任意一条直线都是某个一次函数的图象呢?
2、一次函数、二元一次方程、直线三者有着紧密的联系,我们既可以用函数的方法来处理方程的问题,也可以从方程的观点来讨论函数;既可以用坐标平面上的直线来表示一次函数与二元一次方程,也可以用方程和函数的思想来研究直线的性质,以及直线与直线之间的关系.
3、数形结合是解函数问题的重要思想方法,它包括两方面内容:
(1)由数定形
即通过函数解析式的系数符号,确定图象的大致位置.
(2)由形导数
即从给定的函数图象上获得解的信息,如图象的大致位置;确定解析式中系数符号;图象上的点的坐标等.
4、一次函数的图象是一条直线,对于实际问题,由于自变量的取值范围受实际意义的限制,因此,作出的函数图象是常见直线的一部分,相应函数值就有最大值或最小值.
5、一次函数是表示日常生活中匀速变化的两个变量之间关系的数学模型,是最基本的函数,有着广泛的应用价值. 运用一次函数解题时应注意:
(1)一次函数的图象是一条直线.
(2)函数解析式 中的系数符号,确定图象的大致位置及y随x变化的性质.
(k>0,b>0) (k>0,b<0) (k<0,b>0) (k<0,b<0)
(3)确定一次函数解析式,通常需要两个独立的条件.
(4)一次函数与二元一次方程有着密切的联系,任意一个一次函数y=kx+b 都可以看做是一个关于x,y的二元一次方程kx-y+b=0;反过来,任意一个二元一次方程ax+by+c=0 ,当 时,可化为形如y=-ax/b-c/b 的函数形式.
例题与求解
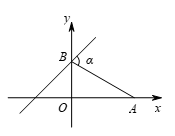
【例1】(1)如图,已知A点坐标为(5,0),直线 y=x+b(b>0)与y轴交于点B,连接AB,∠α=75° ,则b= .
(2)一次函数y=ax+b的图象l1关于直线y=-x轴对称的图象l2的函数解析式是 .
【例2】已知 abc=0,并且(a+b)/c=(b+c)/a=(c+a)/b=p,则直线 y=px+p一定通过( )
A.第一、二象限 B. 第二、三象限 C. 第三、四象限 D. 第一、四象限
【例3】如图,△AOB为正三角形,点B的坐标为(2,0) ,过点C (-2,0)作直线l 交AO于D,交AB于E,且使△ADE和△DCO的面积相等,求直线l 的函数解析式.
【例4】某科技公司在甲地、乙地分别生产了17台、15台同一种型号的检测设备,全部运往大运会赛场A,B两馆,其中运往A馆18台、运往B馆14台. 运往A,B两馆的运费如下表:
| 出发地
目的地 |
甲地 | 乙地 |
| A馆 | 800元/台 | 700元/台 |
| B馆 | 500元/台 | 600元/台 |
(1)设甲地运往的设备有x台,请填写下表,并求出总运费y(元)与x(台)的函数关系式;
| 出发地
目的地 |
甲地 | 乙地 |
| A馆 | x(台) | (台) |
| B馆 | (台) | (台) |
(2)要使总运费不高于20200元,请你帮助该公司设计调配方案,并写出有哪几种方案;
(3)当x为多少时,总运费最小,最小值是多少?
【例5】已知长方形ABCO,O为坐标原点,B的坐标为(8,6) ,A,C分别在坐标轴上,P是线段BC上的动点,设PC=m ,已知点D在第一象限且是直线 y=2x+6上的一点,若△APD是等腰直角三角形.
(1)求点D 的坐标;
(2)直线 y=2x+6向右平移6个单位后,在该直线上是否存在点D,使△APD是等腰直角三角形?若存在,请求出这些点的坐标;若不存在,请说明理由.
【例6】如图1是甲、乙两个圆柱形水槽的轴截面示意图,乙槽中有一圆柱体铁块立放其中(圆柱形铁块的下底面完全落在乙槽底面上). 现将甲槽中的水匀速注人乙槽,甲、乙两个水槽中水的深度y(厘米)与注水时间x(分钟)之间的关系如图2所示.根据图象提供的信息,解答下列问题:
(1)图2中折线ABC表示 槽中水的深度与注水时间之间的关系,线段DE表示 槽中水的深度与注水时间之间的关系(以上两空选塡“甲”或“乙”),点B的纵坐标表示的实际意义是 ;
(2)注水多长时间时,甲、乙两个水槽中水的深度相同?
(3)若乙槽底面积为36平方厘米(壁厚不计),求乙槽中铁块的体积;
(4)若乙槽中铁块的体积为112立方厘米,求甲槽底面积(壁厚不计).(直接写出结果)
详细答案以及更多习题,请免费下载: