【提招专题】全等三角形 模型5——雨伞模型

全等三角形模型繁杂，本次的内容是全等三角形的第五个模型——雨伞模型。即在几何图形中，如果出现角平分线，那么就要从此入手，找出两个三角形并证明全等。

模型讲解

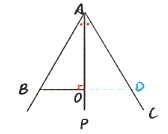
【条件】AP是∠BAC的平分线，BO⊥AP

【结论】①△ABO≌△ADO，②AB=AD，③OB=OD

【证明】

【例题】

已知：如图，△ABC中，AB=AC，∠A=90º，∠ACB的平分线CD交AB于点E，∠BDC=90º，

求证：CE=2BD．

解析以及更多例题请点击：

全等三角形模型5 雨伞模型