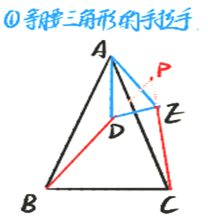
全等三角形模型繁杂,本次的内容是全等三角形的第二个模型——手拉手模型,即两个全等三角形有顶点重合。
那么,如何快速找出有顶点重合的两个三角形并证明它们全等呢?
模型讲解
【结论1】如图所示,AB=AC,AD=AE,∠BAC=∠DAE,则
⑴△ABD ≌△ACE; ⑵BD和CE的夹角∠P=∠BAC=∠DAE.
(1)△ABD ≌△ACE,证明如下:
(2)BD和CE的夹角∠P=∠BAC=∠DAE. 证明如下:
【结论2】如图所示,AB=AC,AD=AE,∠BAC=∠DAE=90º,则
⑴△ABD ≌△ACE; ⑵BD⊥CE
(1)△ABD ≌△ACE,证明如下:
(2)BD⊥CE, 证明如下:
【结论3】如图所示,△ABC与△DCE是等边三角形,则
⑴△BCD ≌△ACE; ⑵∠AOB=∠DOE=60º
【结论4】如图所示,△ABC与△DCE是等边三角形,当点B、C、E共线时:
更多信息,免费下载以下文档: