全等三角形是初中几何的基础内容。虽然基本证明公理计较简单,但是在较复杂模型中,要能快速和准备应用全等三角形模型,仍然是一件不容易的事情。
全等三角形的好处是,通过三角形全等,可以实现由边相等证明角相等,或者由角相等证明边相等。这个转换,有时候是无可替代的。
今天给大家带来—— K型模型
全等三角形 模型(一)—— K型模型
| 模型讲解 |
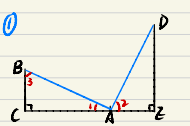
【结论1】如图所示,AB⊥AD且AB=AD,BC⊥CE,DE⊥CE.
则△ABC≌△DAE,CE=DE+BC.
【证明】∵BC⊥CE,DE⊥CE,AB⊥AD,
∴∠C=∠BAD=∠E=90°,
∴∠1+∠3=∠1+∠2=90º,∴∠2=∠3
在△ABC和△DAE 中,
∠C= ∠E=90°
∠2=∠3
AB=DA,
∴在△ABC≌△DAE(AAS),
∴AC=DE,BC=AE,
∴CE=CA+AE=BC+DE.
【结论2】如图所示,AB⊥AD且AB=AD,BC⊥CA,DE⊥CA.
则△ABC≌△DAE,CE= DE –BC.
【证明】 证明同上,△ABC≌△DAE,AC=DE,BC=AE
CE= AC –AE= DE –BC.
更多信息,免费下载以下文档: