1.如图,在ΔABC中, AB=2,∠ABC=60°,∠ACB=45°,D是BC的中点,直线经过点D,,,垂足分别为E,F,则AE+BF的最大值为( ) A.√6 B.…
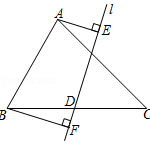

1.如图,在ΔABC中, AB=2,∠ABC=60°,∠ACB=45°,D是BC的中点,直线经过点D,,,垂足分别为E,F,则AE+BF的最大值为( ) A.√6 B.…
1.法国数学家费马提出:在内存在一点P,使它到三角形顶点的距离之和最小。人们称这个点为费马点,此时PA+PB+PC的值为费马距离。经研究发现:在锐角中,费马点P满足,如图,点P为锐角的费马点,且P…
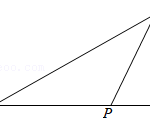
1.如图,在中,,,P为AC边上的一个动点(不与A、C重合),连接BP,则的最小值是( ) A. B. C. D.8 2.中,,,,若点D是边BC 上的动点,…
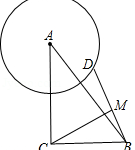
1.如图,在中,,,,点D是以点A为圆心、4为半径的圆上一点,连接BD,点M为BD中点,则线段CM长度的最大值为 A.7 B.8 C.6 D.5 …
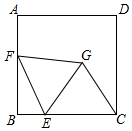
1、如图,正方形ABCD的边长为7,E为BC上一点,且BE=,F为AB边上的一个动点,连接EF,以EF为边向右侧作等边△EFG,连接CG,则CG的最小值为_____. 2、如图,矩形ABCD中,A…
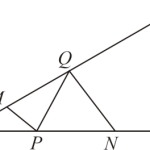
1.如图,在中,,,,平分,点P、Q分别是AB,ADAD边上的动点,则的最小值是( ) A.4 B.5 C.6 …
1.已知,,,则a,b,c的大小关系是( ) (A)c<b<a (B)b<a<c (C)b<c<a (D)a<b<c 2.因式分解x2+…
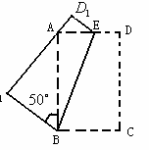
1.如图,已知DE∥BC,CD与BE相交于点O,并且S⊿DOE:S⊿COB=4:9, 则AE:AC=( ) (A)4:9 (B)2:3 (C)3:2 (D)9:4 2.如图:将一个矩形纸片AB…
1.已知点E,F,A,B在直线上,正方形EFGH从如图所示的位置出发,沿直线向右匀速运动,直到EH与BC重合。运动过程中正方形EFGH与正方形ABCD重合部分的面积 S 随时间 t 变化的图像大致…