阅读与思考
梯形是一类具有一组对边平行而另一组对边不平行的特殊四边形,梯形的主要内容是等腰梯形、直角梯形等相关概念及性质.
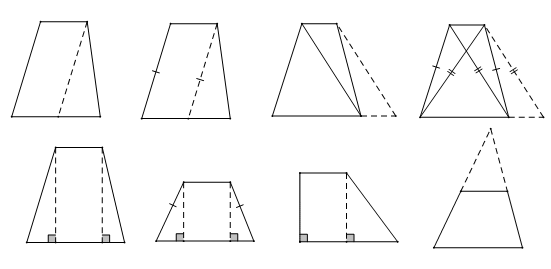
解决梯形问题的基本思路是:通过适当添加辅助线,把梯形转化为三角形或平行四边形,常见的辅助线的方法有:
(1)过一个顶点作一腰的平行线(平移腰);
(2)过一个顶点作一条对角线的平行线(平移对角线);
(3)过较短底的一个顶点作另一底的垂线;
(4)延长两腰,使它们的延长线交于一点,将梯形还原为三角形.
如图所示:
例题与求解
【例1】如图,在四边形ABCD中,AB//CD,∠D=2∠B,AD和CD的长度分别为 a,b ,那么AB的长是___________.
【例2】如图1,四边形ABCD是等腰梯形,AB//CD.由四个这样的等腰梯形可以拼出图2所示的平行四边形.
(1)求四边形ABCD四个内角的度数;
(2)试探究四边形ABCD四条边之间存在的等量关系,并说明理由;
(3)现有图1中的等腰梯形若干个,利用它们你能拼出一个菱形吗?若能,请你画出大致的示意图.
【例3】如图,在等腰梯形ABCD中,AD//BC,AB=DC,且AC⊥BD,AF是梯形的高,梯形的面积是49cm2,求梯形的高.
【例4】 如图,在等腰梯形ABCD中,AB//DC,AB=998,DC=1001,AD=1999,点P在线段AD上,问:满足条件∠BPC=900的点P有多少个?
【例5】 如图,在等腰梯形ABCD中,CD//AB,对角线AC,BD相交于O,∠ACD=600,点S,P,Q分别为OD,OA,BC的中点.
(1)求证:△PQS是等边三角形;
(2)若AB=5,CD=3,求△PQS的面积;
(3)若△PQS的面积与△AOD的面积的比是7:8,求梯形上、下两底的比CD:AB.
【例6】如图,分别以△ABC的边AC和BC为一边,在△ABC外作正方形ACDE和CBFG,点P是EF的中点,求证:点P到边AB的距离是AB的一半.
更多例题与解析,请免费下载: