全等三角形模型繁杂,本次的内容是全等三角形的第六个模型——半角模型。半角即一个角的度数是另一个角度数的一半,无论是三角形、正方形还是不规则四边形,都有半角的出现,本次讲解的内容是根据几何图形中的半角条件,证明两个三角形全等并解决实际问题。
模型讲解
一、正方形中的半角模型
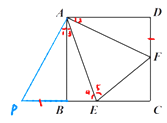
【条件】如图①两个角共顶点,②其中一个角(45º)是另一个角(90º)的一半
【结论】①EF=BE+DF, ②EA平分∠BEF,FA平分∠DFE,
③△EFC的周长等于正方形边长的2倍
④ 如图:AM=AB
⑤ 如图:∠EAF=45º,则EF²=BE²+FC²
【证明】①∶延长CB至点P,使得BP=DF 连接AP
第一次全等 第二次全等
在△ABP和△ADF中 在△AEP和△AEF中
(1)AB=AD(正方形边长相等) (1)AP=AF
(2) ∠ABP=∠ADF=90º (2)∠PAE=∠FAE
(3)BP=DF(构造) (3)AE=AE
∴ △ABP≌△ADF(SAS) ∴△AEP≌△AEF(SAS)
∴AP=AF ,∠1=∠2 ∴PE=EF
∵∠2+∠3=45º 即PB+BE=EF
∴∠1+∠3=45º, ∴DF+BE =EF
∴∠PAE=∠FAE
② 由①得:△AEP≌△AEF,则∠4=∠5,∠AFE=∠P
又△APB≌△AFD,∴∠P=∠AFD,∴∠AFE=∠AFD
∴EA平分∠BEF,FA平分∠DFE
③ 由①得:EF=BE+DF,∴△EFC的周长=EF+EC+CF=BE+DF+EC+CF
=BC+DC, ∴△EFC的周长等于正方形边长的2倍
④ 过A作AM⊥EF,则∠AME=∠B=90º。由①得∠1=∠2,AE=AE,
∴△ABE≌△AME(AAS),∴AM=AB
⑤ 如图,过点A作AP⊥AF 且AP=AF.连接PE
∵∠CAB= ∠PAF=90º,∠1=∠2
第一次全等 第二次全等
在△ABP和△ACF中 在△AEP和△AEF中
(1)AB=AC (1) AP=AF
(2) ∠2=∠1 (2)∠PAE=∠FAE
(3)AP=AF (3) AE=AE
∴ △ABP≌△ACF(SAS) ∴△AEP≌△AEF(SAS)
∴BP=CF ,∠ABP=∠C=45º ∴PE=EF
∵∠EAF=45º 在Rt△PBE中,PE²=PB²+BE²
∴∠1+∠3=45º, 即EF²=CF²+BE²
∴∠2+∠3 =45º
二、等腰三角形中的半角模型
【条件】 如图,△ABC是等边三角形,△BDC 是等腰三角形,
且∠BDC=120°,∠MDN=60º,
【结论】①MN= BM+CN;
②△MAN 的周长等于△ABC边长的 2 倍;
③MD是∠BMN的平分线,ND是∠CNM的平分线
【证明】
∵△BDC是等腰三角形,且∠BDC=120°,
∴∠BCD=∠DBC=30°.
∵△ABC是等边三角形,∴∠ABC = ∠BAC = ∠BCA=60°,
∴∠DBA= ∠DCA=90°.
延长 AB至点F,使BF=CN,连接DF,如图.在△BDF 和△CDN 中,DB=DC,∠DBF=∠DCN,BF=CN,∴△BDF≌△CDN(SAS),
∴∠BDF=∠CDN,∠F=∠CND,DF=DN.
∵∠MDN=60°, ∴∠BDM+∠CDN=60°,∴∠BDM+∠BDF=60°,
即∠FDM=60°=∠MDN.
在△DMN 和△DMF 中,DN=DF,∠MDN= ∠MDF, DM=DM,
∴△DMN≌△DMF(SAS),∴ MN=MF=BM+CN,
∠F=∠MND=∠CND,∠FMD=∠DMN,
∴△AMN的周长是 AM+AN+MN=AM+MB+CN+AN=AB+AC=2边长.
三、对角互补且邻边相等的半角模型
【条件】如图,∠B+∠D=180°,∠BAD= 2∠EAF,AB=AD,
【结论】①EF=BE+FD;
②EA 是∠BEF的平分线,FA是∠DFE的平分线.
更多习题及解析请点击: