暑假期间,很多同学自学了《轴对称图形》这一章节。轴对称图形虽然看起来简单,但其实对解决问题帮助很大。
今天给大家介绍利用轴对称思想解决最值问题的经典方法——将军饮马。
平面几何中涉及最值问题的相关定理或公理有:
① 线段公理:两点之间,线段最短. 并由此得到三角形三边关系;
② 垂线段的性质:从直线外一点到这条直线上各点所连的线段中,垂线段最短. 在一些“线段和最值”的问题中,通过翻折运动,把一些线段进行转化即可应用 ①、② 的基本图形,并求得最值,这类问题一般被称之为“将军饮马”问题。
问题提出:
唐朝诗人李欣的诗《古从军行》开头两句说:“白日登山望烽火,黄昏饮马傍交河.”诗中隐含着一个有趣的数学问题.
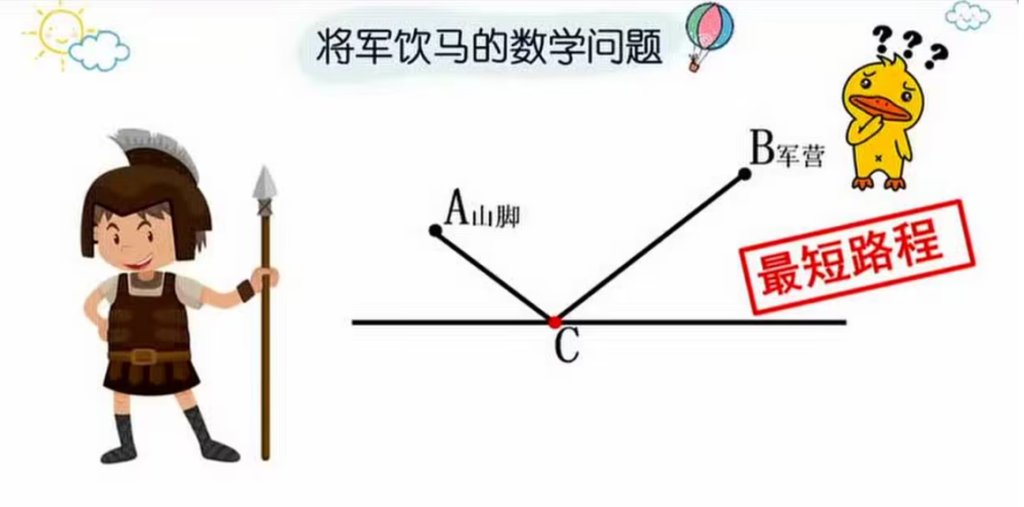
如图所示,诗中将军在观望烽火之后从山脚下的A点出发,走到河边饮马后再到B点宿营.请问怎样走才能使总的路程最短?
详见文档: