【数学文化】第一次数学危机——无理数的发现

1.毕达哥拉斯学派

毕达哥拉斯学派是公元前6世纪末到公元前5世纪初的古希腊哲学家、数学家和神秘主义者毕达哥拉斯及其信徒组成的一个学派，也被称为南意大利学派。

他们的主要特点是把数视为宇宙万物的本原和本质，认为一切物质和现象都可以用整数或整数之比来解释和表达，从而揭示出宇宙的和谐和秩序。

他们的思想对后来的西方哲学和数学有很大的影响，也引发了一些数学和哲学的问题和矛盾，比如无理数的存在和数与形的分离。

2.毕达哥拉斯定理（中国称为勾股定理）

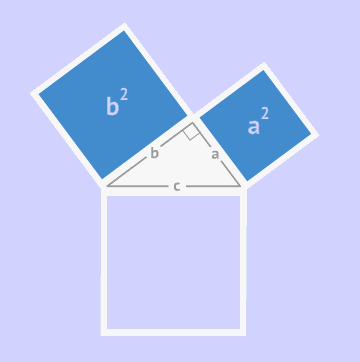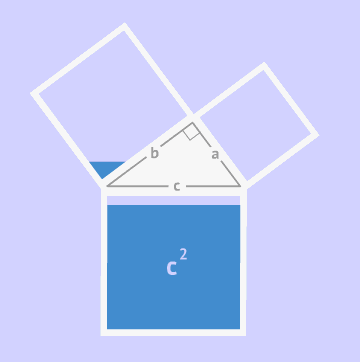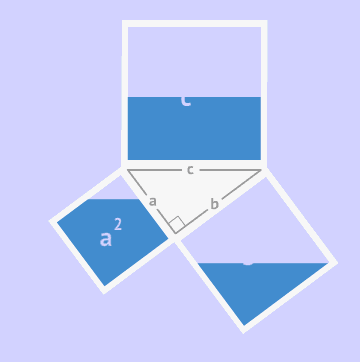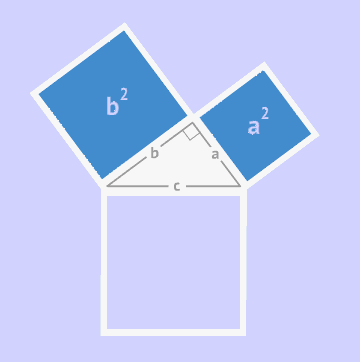
直角三角形的两条直角边的平方和等于斜边的平方. 即两直角边为 a、b ，斜边为c ,则 a²+b²=c².

3.希伯斯与第一次数学危机

毕达哥拉斯的学生希伯斯观察到等腰直角三角形：如果两条直角边都是1，斜边长度不是整数，也不能用两个整数之比表示.
毕达哥拉斯学派的门徒认为希伯斯的发现破坏了学派的信条，导致学派所建立起来的数学体系整体崩塌，危害学派的利益，便把他扔进了大海。鉴于这一发现对当时数学认知的重大动摇，后人称为“第一次数学危机”。
希伯斯在几何图形中发现无理数，付出了生命的代价。但毫无疑问，这次探索是对人类认知的一次卓越贡献。这个危机直到两千年后才得到解决，数学家用有理数来定义无理数，并证明了无理数的存在。