碰到大数字的题目,先简化成小数字来找规律;碰到复杂算周长题目,先简化成简单的一段一段的线段来计算;碰到复杂的求面积的题目,先分解成一个一个的规律图形。
总之,通过知识的小台阶上去,或者通过简单的题目,简单的方法,训练一下解解题能力后,再举一反三。
孩子的解题能力,人的思维、逻辑能力,就是这么训练的。
这是我当年很能啃难题,数学上显得很牛逼的一个关键点。
实际上,数学家,也是这么完善数学世界,解决现实中的问题的。
到中学的时候,我已经有一套直觉一样的技能:可以从简单题目积累经验和记忆,延伸外延到推衍出来一些复杂定理;或者碰到较为复杂的题目,能从大脑中提取搞定接近的简单题目的经验,分解组合搞定难题;更或者,碰到难题,能动手设计一个简化后的题目,从解决这个简单题目中,获得搞定难题的启发,顺利搞定难题。
小明有360颗糖,小红有120颗糖。小明每次给小红4颗糖,请问,需要给几次,两人的糖能一样多?
小明有36颗糖,小红有12颗糖。小明每次给小红4颗糖,请问,需要给几次,两人的糖能一样多?
最开始,小明糖36, 小红糖12; 两人差距24;
小明给第1次后,小明糖32,小红糖16;两人差距16;
小明给第2次后,小明糖28,小红糖20;两人差距8;
小明给第3次后,小明糖24,小红糖24;两人差距0。
哎呀,解决了这个简单问题,我们就发现了,每次两人的数量差距减少8。这是一个重要的规律。
36-12=24,每次差距8,那就是24除以8=3次。看看我们的实验,也确实是3次。
那么,再回到最初的题目,360-120=240,每次差距8,240除以8=30次。搞定。
当然,对小孩子,我们只能先教一个经验,大数字先变成小数字来做实验。
嗯,以前一直强调,数学要用草稿纸。就是我觉得:数学也是有实验的。只不过,实验器材是草稿纸,铅笔,还有大脑。嗯,后来增加了圆规、三角板、直尺、计算器、计算机……等等。
孩子来请教我难题,我也一般会这么示范如何解题。很耐心,先找一道接近的简单题开始讲,或者让孩子琢磨先。
既说明了,面对问题,先动手实验,从简化的题目开始是个好方法;
又说明了,在数学解题实验(实践)中,找规律的重要性;
代数和几何,亲如一家,还有一道经典题,那就是梯形的面积计算公式。
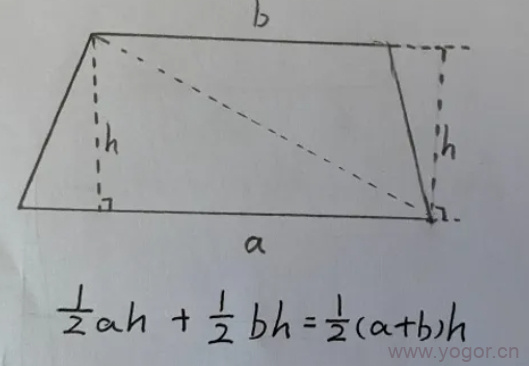
而这两个三角形,按三角形面积公式:分别是:1/2*a*h,1/2*b*h。
那么,如下图推导,就得到了梯形面积公式1/2(a+b)h。
或者反之,由代数公式,用分配律分解一下,可以看到,梯形可以分解成两个三角形。
(1)给孩子开了脑洞:哦,梯形的面积公式,还有这样一层意义。
(2)当孩子课内吃不饱,去学梯形的一半模型的时候,孩子会自然发现,哦,h变成了1/2h,两个面积之和,当然是一半了。
很自然打通了课内和课外奥数之间的关系。省心省事,还体会了代数和几何亲如一家之美。
何乐不为,家长一定要先理解,然后告诉孩子啊,这个很简单,每个家长都应该能理解。
三角形其实是梯形的特殊情况,也可以给孩子发散发散。
一旦梯形的上底长度为0,不就是一个三角形的面积公式了啊。
数学建模中,我们先从简单的开始,逐步走向复杂,但复杂情况中,如何回到简单,孩子也要思考下。
这也是让孩子大脑展开丰富的联想和联系的一个角度啊。而这种思维锻炼,非常必要。
比如,某年师达小升初题目:三角形的两个内角之和等于91度,请问,这个三角形是锐角三角形不?
答案是不一定:因为有一个角,可能是90度,也可能是90.5度。
(1)三角形的两个内角之和等于91度,请问,这个三角形可以是直角三角形不?
(2)三角形的两个内角之和等于91度,请问,这个三角形可以是钝角三角形不?
那么,你有了这样的思考,下面的题目,自然就简单了:
一个三角形最小的锐角是50°,这个三角形一定是( )三角形
我们当年就习惯这样,一道题做了之后,想一想,如果换成另外一种题目,我会不会。
我们那个时代,接触的题目很少,只好这样自己给自己出题,自己变换题目来做。
上面的题目,还是差不多的题,考的是同一个想象力。有的题目,改一改,增加或者降低了难道,或者变成了更加综合的题目。
比如,三角形三条边都是正整数。如何判断三角形是钝角,还是直角,还是锐角三角形呢?这个题,就是数论和几何的综合了。
课后延伸题:最长边为正整数8的三角形,有多少种情况?
有一个三角形,三条边都是正整数,已知最长边为8,请问,这样的三角形,会有多少种?
如果最长边是12,最长边是13,最长边是n呢?各会有多少种情况??
这个题目,就是先做简化的,再找规律做复杂的题目的一个经典题。
本文由友果分享提供。友果培优,复旦名师执教,小学/初中/高中。联系电话/微信:17751295132


